Binary Search 🔍 And Big 0️⃣ Notation

January 02, 2022

In my previous blog we’ve had seen that what is Data Structures and Algorithms are, and also have looked into an example of Jhon and Ana by playing a game of guessing a number and by observation we concluded that Jhons approach is called Linear Search whereas Ana’s approach is called Binary Search.

Binary Search

In real use case of binary search the algorithm wouldn’t return the target value because we already know that. It’s a search algorithm, so we are already providing something to search for, instead what it returns is the position in the list that target occupies.

without the list being sorted a binary search algorithm would discard all the values on the left of target value. Therefore the 🧠necessary condition for binary search is that list of values must be sorted.

Formal defination of Binary Search 🔍

🪜 Steps of Binary Search

Determine the middle position of the sorted list.
Compare the element in the middle position to the target element.
If the element match, we return the middle position and end the algorithm. if they didn’t match then 👇
Check wether the element in the middle portion is smaller than the target element if it is then we go back to step 2 with a new list that goes from the middle position of the current list to the end of the current list.
If the element in the middle position is grater than the target element then again we go back to step 2 with a new list that goes from start of the current list to the middle position of current list.
- We repeat this process until the target element is found or until a sub list contains only one element.
- If that single element sublist does not match with target element then we end the algo indicating “element does not exist.”

Efficiecy of Binary Search

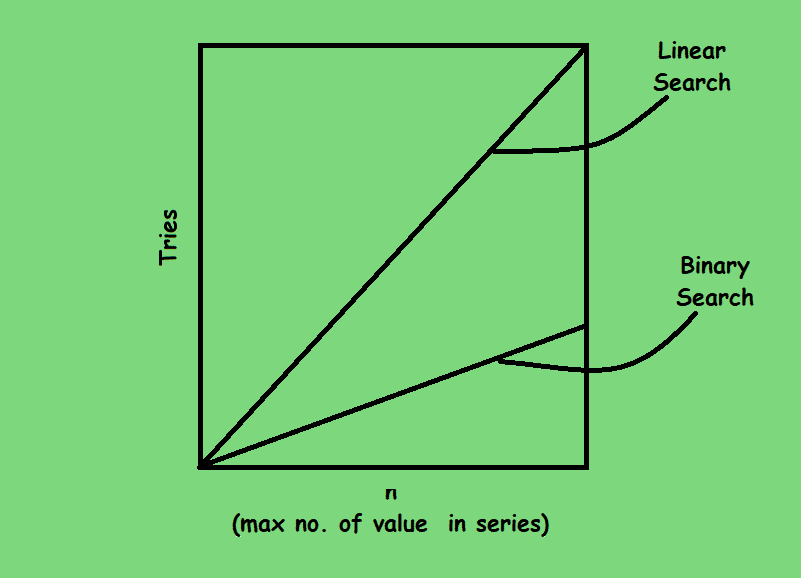
The above plot shows the growth rate of the algorithm also known as the order of growth. Different algorithms grow at different rates and by evaluating growth rates we get a much better picture of their performance because we know how the algorothm will hold up as “n” larger.

Big 0️⃣ Notation.

Theoritical defination - Complexity of an algorithm as function of the size.

Breakdown of the theoritical defination could be done as-

Big O is a notation used to describe complexity.
Notation here means that it simplifies everything we have talked about down into a single variable (Which is 0️⃣).
An example of complexity written in terms of big O look lile this ➡️ O(n) where O is the order of magnitude of complexity.

⁉️ If it takes Ana 4 tries when n(target) is 10. how long does the the algorithm take when n(target) is 10 million.🤯

♒ When we use Big O for this the variable used (which we will get to) distills that information down so that reading the variable you get a big picture without having to plot graphs.

✳️ Complexity is relative.

Big O is very usefull notation when camparing time and space complexity but only when comparing amongst algorithms that solve the same problem.

✳️ The last bit in the function of Big O is a “A function of size” and all this means is that Big O measures complexity as the input size grows.

You will also see Big O referred to as the upper bound of the algorithm and what that means is that “Big O measures how the algorithm performs in the worst case scenerio”.

In a nutshell Big O is just a notation that condenses the data points and graphs down one variable.

What this variable looks like for:
- Linear search : We say that it has time complexity of Big o of n ➡️ O(n).
- Binary search : We say that it has a time complexity of Big O of log(n) ➡️ O(logn)

In our discussion of complexity we made one assumption that the algorithm as whole had a single measure of complexity.

♒ Each step in the algorithm has its own space and time complexity.
♒ In linear search for example there are multiple steps and the algorithm goes like this, Start at the beginning of the list or range of values compare the current value to the target if the current value is the target value we are done, if its not we will move on sequentially to the next value in the list and repeat step 2.

✳️ Let’s go back to step 2 “Comparing the current value to the target, does the size of dataset matters for this step? When we are at step 2 we are already at that position in the list and all we are doing is reading the value to make a comparision.”
♒ Reading a value is a single operation and if we were to plot it on a graph of runtime per operations against “n”, it looks like this👇 “a straight line”

“A straight line” that takes constant time regardless of the size of ‘n’. Since this takes the same amount of time in any given case, we say that the run time is constant time. In Big O notation we represent this as O(1).

⁉️ How to read O(1)? It is read as constant time.

So reading value in a list is a constant time operation.

This is the most ideal case when it comes to run times because input size does not matter, and we know that regardless of the size of n the algorithm runtime will remain the same.

For Binary Search

When played a game (Guessing of numbers) using Ana’s approach we noticed that with every we were able to discard half the data . But there’s another pattern that emerges that we didn’t explore 🤯🤯.

Let’s say n(target) = 10, how long does it take to find an item at 10^th position of the list.

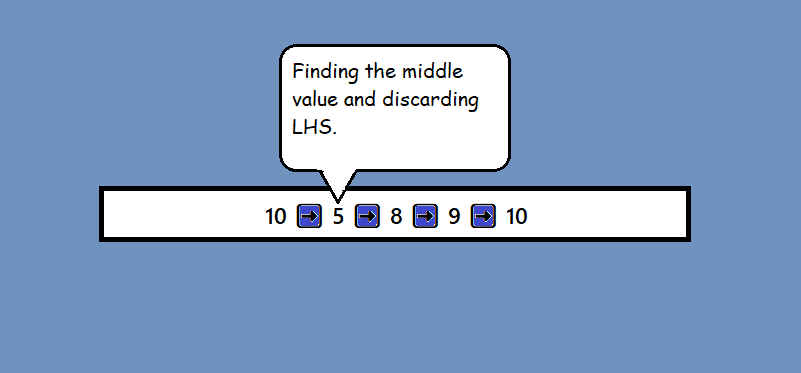
When n=20

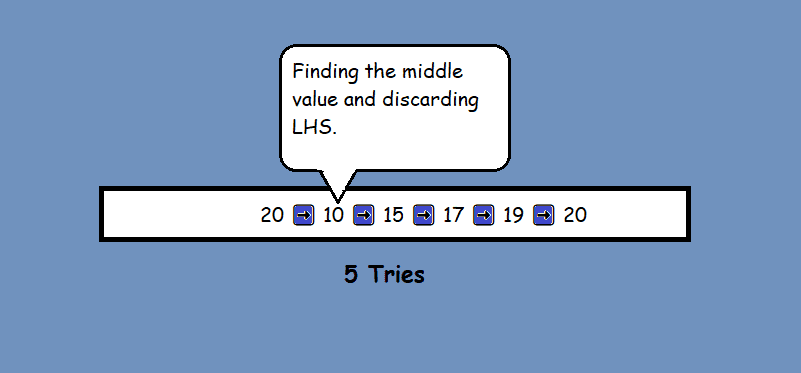
now lastly 😴 for n = 40

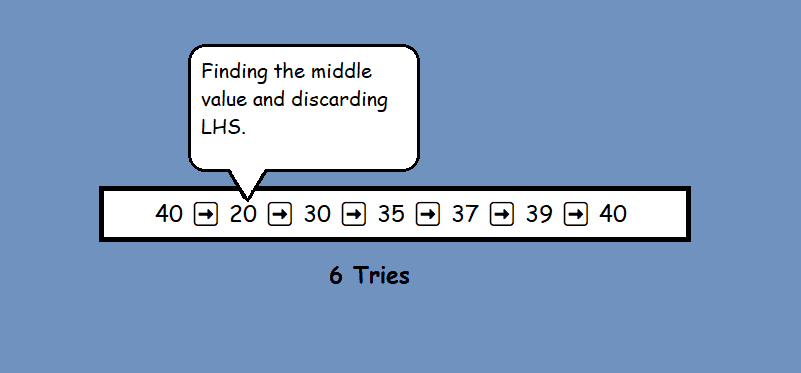
➡️ Note: That every time we doubled the value of n the number of operartions it takes to reduce the list down to a single element only increase by ‘1’.

There is mathematical relationship to this pattern and its called logarithm of n

⁉️How?

Explaination for logarithm

2 times 1 is 2 ➡️ 2¹ = 2

2 x 2 = 4 ➡️ 2² = 4

2 x 2 x 2 = 8 ➡️ 2³ = 8

Exponents define how a number grows with 2 raised to the power 3 we start with bare value and multiply itself with 3 times.

The inverse of an exponent is called a logarithm.

So if I say log to base 2 of 8 equals 3

log₂8 = 3

So I am saying basically the opposite of an exponent, instead of saying how many times do I have to multiply this value, I am asking how many times do I have to devide 8 with 2 to get the value 1.

This takes 3 operations.

If n was 16, how many tries does it take to get to that last element, well we start in the middle at 8 that’s too low so we move to 12 then we move to 14 then to 15 and then to 16 which is 5 tries or log16₂ + 1.

In general for a given value of n the number of tries ot takes to find the worst case scenerio is log(n) + 1 and because this pattern is overall a logarithmic pattern we say that the runtime of such algorithmsis logarithmic if we plot these data points on our graph a logarithmic runtime it looks like this 👇

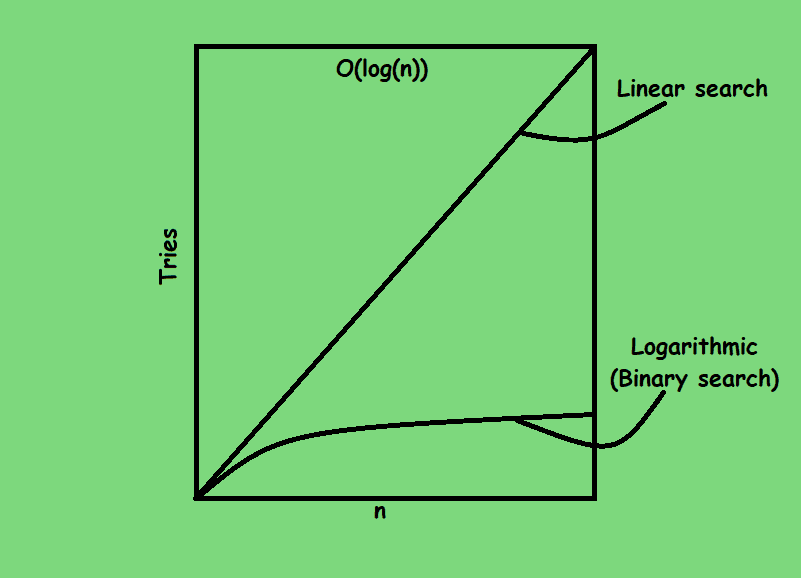
In Big O notation we represent a logarithmic runtime as O(log(n)) or O(ln(n)) read it as logarithmic time

As n grows very large the number grows very slowly and eventually plattens out.
since this line is below the line for linear runtime, you might often hear algorithms with logarithmic runtimes being called sublinear.
Logarithmic or sublinear runtime prefreed to linear because they are more efficient but in practice linear search has its own set of advantages.